こんにちは。
相変わらず canvas タグとにらめっこしているエンジニアの辻です。
前回は様々な線形変換を見てきました。
今回は線形変換の関数を実行する上で重要なポイントを 1 つ紹介します。
ソースコードは以下になります。
ただ今回はソースを確認せずとも大丈夫です。このまま記事を読み進めていただいてOKです。
「60° 反時計回りに回転 → x 軸に対して反転」した点 A と 「x 軸に対して反転 → 60° 反時計回りに回転」した点 B の違いは?
まず下図をご覧ください。
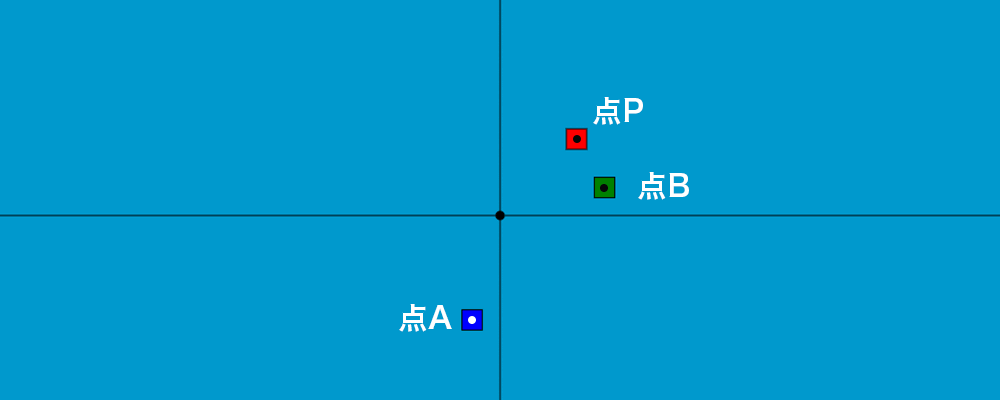
x: 75, y: 75 の点 P を
60° 反時計回りに回転後に x 軸に対して反転させた点 A と
x 軸に対して反転後に 60° 反時計回りに回転させた点 B を
canvas に描画した結果です。
(※回転は原点を軸にしています。)
ご覧の通り、点 A と点 B は異なる点になります。
さて、ここで 1 つ思考実験をしてみましょう。
点 A、点 B は変換前の点が一緒です。どちらも点 P (75, 75)を元に変換を行っています。
そして、60° 回転させる処理と、x 軸に対して反転させる処理も共通です。
…なのに、なせ計算結果が異なるのでしょうか。
一般的なイメージとして、同じ値に対して同じ値を乗算したら、計算結果は一緒になりますよね。
x * y * z は、xyz だろうが、zyx だろうが、yzx だろうが、結果は一緒です。
ですが、点 A と点 B で描画位置が異なります。
一体これはなぜなのでしょう。
バグなのでしょうか。
…いいえ、これはバグではありません。
点 A と点 B が異なるのは正しい挙動です。
なぜこんな結果になるのかというと、行列積のある特徴が関係しています。
行列積は計算する順番によって結果が異なる
行列積には以下の特徴があります。
行列 A と行列 B があるとします。
- 行列積 AB は、かけられる行列 A の列数と、かける行列 B の行数が一致している場合のみ定義される。
- 行列積 AB が定義されていたとしても、BA が定義されているとは限らない。
- 仮に行列積 AB と BA が定義されていたとしても、AB = BA が成り立つとは限らない。
今回最も重要になるのは、3 番目の特徴です。
スカラーの計算であれば、乗算に順序は関係ありません。
x と y と z を乗算する時、順序を入れ替えても計算結果は変わりません。
しかしながら、この点において行列は異なります。
AB = BA が必ずしも成り立つわけではないのです。
つまり「行列積は計算する順番によって計算結果が異なる」という事です。
(B が単位行列の場合…など等式が成り立つ場合もありますが、今回は割愛します。)
この点を踏まえて、前半の点 A、点 B を改めて考えてみましょう。
まず今回行っている変換は、以下の 2 つです。
- 60° 反時計回りに回転させる
- x 軸に対して反転させる
1、2の変換をそれぞれ f、g としましょう。
点 P に変換 f を行う f(p)と、点 P に変換 g を行う g(p) を計算式で表すと以下の通りです。
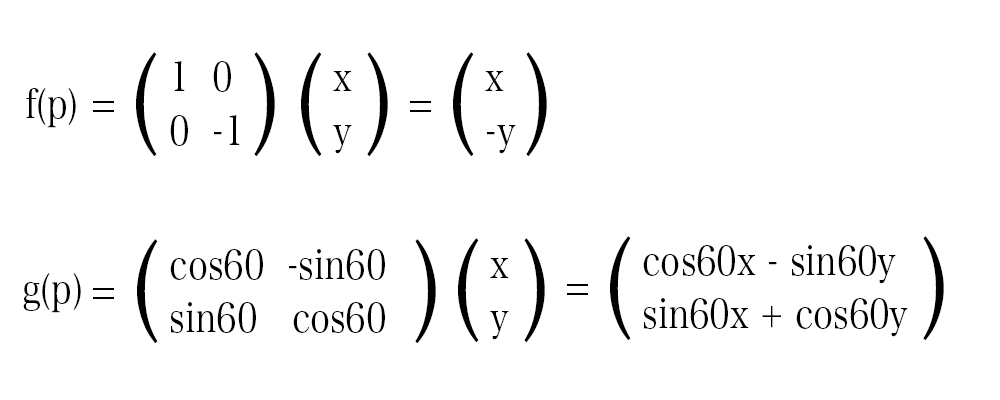
次に、 f(p)と g(p)の計算結果にそれぞれ変換 g と f を行います。
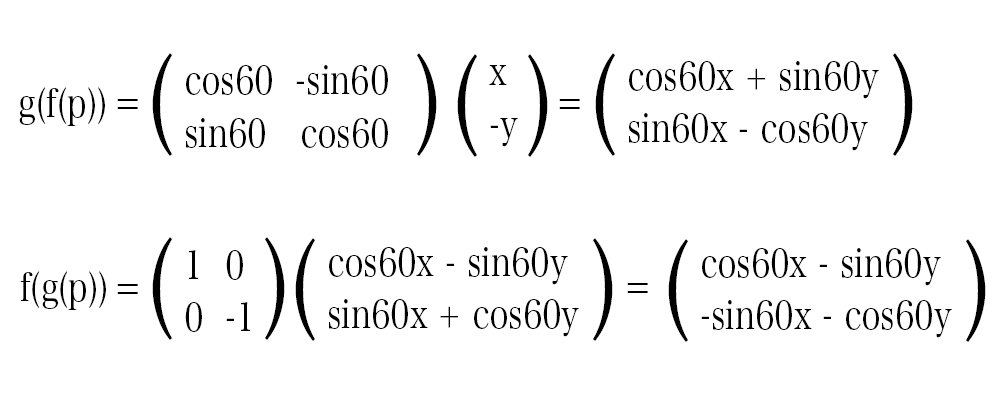
f(g(p))(点 A) と g(f(p))(点 B) の計算結果が異なりますね。
このように行列積は、計算する順番によって結果が異なるのです。
最後に点Pの座標である x= 75, y= 75 を代入してみます。
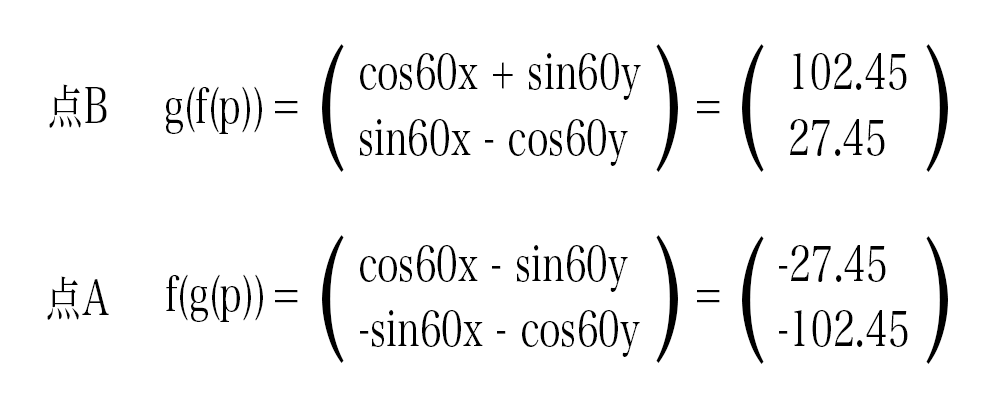
これで点 A、B の位置が算出されました。
点 A、B はだいたい(-27.45, -102.45)、(102.45, 27.45)の位置にいる事が分かりました。
以上の事から得られる教訓は「canvas で複数回の線形変換を行う時は、順番に気をつけよう」です。
「同じ処理を噛ませたら、結果も同じになるでしょ」と思っていると、意図しない位置に描画されてしまいます。
行列積をしっかりとイメージすることが大切ですね。
まとめ
今回は行列積の特徴から、線形変換の実装のポイントを紹介しました。
ちなみに、今回のような複数回の変換を行う事を合成変換といいます。
もっと詳しく知りたい方は wikipedia をご覧ください。
行列 – wikipedia
それでは、また!